| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 오픈텔레미트리
- 왜 쿠버네티스
- Kubernetes Architecture
- controller manager
- opentelemetry
- 쿠버네티스 구조
- Kubernetes User
- 기저조건
- Data store
- 깃
- Branch
- 쿠버네티스 유저
- 마스터 노드
- container runtime
- 쿠버네티스 네터워크
- k8s
- 종결 조건
- 워커 노드
- worker node
- smart money
- 장단기 금리 차
- 컨테이너 런타임
- Instrumentation libraries
- 쿠버네티스
- 워커 노드 구조
- Dag
- COMMIT
- worker node architecutre
- master node
- GIT
- Today
- Total
개발과 잡지식
Algo02 - 탐색 알고리즘 - 0 선행 개념 본문
탐색 알고리즘 - 0 선행 개념
define
탐색 알고리즘 이라면 무엇을 탐색 하려는 걸까?
그래프 혹은 트리 이다. 어떤 상황에서 쓰고 싶은지에 따라서 다르겠지만 둘다 사용 가능하다.
그래프와 트리는 컴퓨터 전공인 이라면 한번쯤은 봤을 단어 들이다. 이는 많은 사람들의 동의 할 것 같다.
그렇다면 지금 바로 트리와 그래프의 차이가 무엇인지 말해 달라고 하면 말 해 줄 수 있나요?
없다면 다시 한번 짚고 가던지 검색 해보시는 걸 추천 합니다.
DAG이라고 떠오른 분들은 이번 글은 생략 하셔도 좋을 것 같습니다.
그래프
출처 : https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%9E%98%ED%94%84_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)

그래프는 간단하게 vertex, edge의 조합으로 이루어 진다.
vertex는 위의 그림에서 동그라미 들이다. -정점
edge는 위의 그림에서 검정색 선을 말한다. -간선
vertex들을 연결한 간선, 방향 있을(유향) 수도 없을 (무향)수도 있으며, 가중치가 있을 수도 없을 수도 있다.
이 두가지로 딱히 규칙 없이 이루어진 것 들을 그래프 라고 한다.
하나의 vertex 에서 나온 간선이 자기 자신을 다시 가리켜도 된다.
graph <- 링크를 눌러보면 수 많은 형태의 그래프 들의 존재 한다는 것을 알 수 있다.
트리
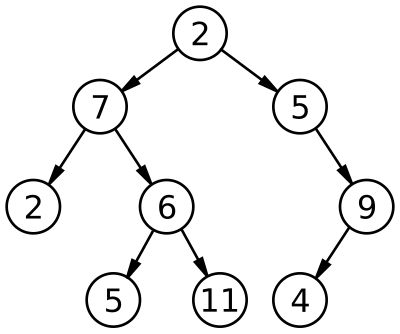
출처 : https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EA%B5%AC%EC%A1%B0
트리도 vertex와 edge를 가지고 있으며 vertex를 노드라고 부르기도 한다.
그리고 여러가지 조건들이 붙는다.
트리는 무조건 유향인 (방향이 있는) 간선만 존재한다.
- 무조건 방향을 가진 간선들만 존재 하며, 한 노드의 간선이 자기 자신을 가리켜서도 안된다.
서로 다른 노드를 가리키는 방법은 하나만 존재해야 한다.
- 서로 다른 노드에 대해서 바로 가는 길이 있으면 그 길을 제외하고 나머지 길이 존재해서는 안된다.
트리의 맨위에 존재하는 노드를 root node
한 노드에서 edge를 통해 다른 노드를 가리킨다면
edge의 출발점에 있는 노드를 parent node, 도착 점에 있는 node를 child node라고 하며 자식은 무조건 하나의 부모 노드만 가질 수 있습니다. 부모는 여러 자식을 가질 수 있죠.
자식이 없는 트리의 맨 바닥쪽에 있는 node를 leaf node 라고 부른다.
왜 node의 종류와 관계?
명칭이 따로 있는 노드들 혹은 관계는 그 만큼 중요해서라고 보면 된다.
모든 트리에서는 루트 노드를 통해서 나머지들에 접근 하게 된다. 시작 지점이라고 보면 된다.
그리고 리프 노드에서는 더이상 갈 곳이 없는 마지막 노드라는 뜻이다.
부모-자식 관계는 트리는 모든 노드들은 부모 자식 더 나아가 증조 부모 고 부모 등등으로 부모-자식 관계를 통해서 찾아 가기도 하고 특정 값을 구하기도 한다.
DAG
DAG이란 무엇일 까? 이는 어떠한 규칙을 말한다.
DAG : Directed Acyclic Graph
무슨 말이냐면 방향이 있으며 비순환 하는 그래프 라는 뜻으로 어떤 노드에서 어떤 엣지를 통해서 가더라도 자신으로 되돌아 올 수 없는 그래프를 뜻한다.
쉽게 말하면 우선 순위가 정해진 그래프 라고 보시면 됩니다.
학교에서 학과 커리큘럼을 보면 선수 강의 라는 것이 있습니다. 어떤 과목을 듣기 위해서는 그전에 특정 과목들을 수강했어야 하는 그런 것이죠.
아래와 같이
자료 구조 -> | | -> 문제 해결 기법
| -> 알고리즘 -> |
객체지향 -> | | -> 경진대회 알고리즘자료구조 와 객체지향을 들어야 알고리즘 강의를 수강 할 수 있고 알고리즘 강의를 수강해야 문제 해결 기법을 들을 수 있다. 이런게 DAG 구조 입니다.
tip ) 요즘에는 비트코인 들의 이러한 구조라고 하죠 :)
추가 적으로 그래프인데 DAG인 그래프에 root가 하나 뿐인 그래프는 tree가 될 수 있습니다.
(위의 자료구조 , 객체지향 은 2개의 루트 노드가 존재해서 트리가 될 수 없습니다.)
그래프가 트리를 포함하는 관계라고 보면 된다.
정리
그래프와 트리에서 차이를 보시고 머리 속에 트리의 구조 그래프의 구조를 잡고 알고리즘을 다가가야만 합니다.
사실 서로 다른 노드를 연결 하는데 있어서 중복이 있고 없고는 큰 차이가 있습니다.
예를 들어서 가중치가 있는 간선으로 이루어진 트리에서 들어서 노드 2개를 연결하는데 드는 최소 비용을 계산하라고 한다면 그래프에서는 중복 경로 없애기 위해 SCC 드으이 기술을 활용하여 계산하는 등 그래프를 트리로 바꾸기 위한 추가적인 작업이 필요합니다.
더 쉬운 예를 들자면 앞으로 배울 dfs, bfs는 중복 처릴 방지하는 코드를 추가하면 그래프든 트리든 작동하지만 pre,in,post -order 등은 오직 트리에서만 작동하는 코드들 입니다.
'알고리즘' 카테고리의 다른 글
| Algo 04 - 재귀함수란 무엇인가? (0) | 2021.01.14 |
|---|---|
| Algo 03 - 탐색 알고리즘 - 1 DAG (0) | 2020.12.25 |
| Algo 01 - 반복문, 에라토스테네스의 체 (0) | 2020.12.25 |
| Algo00 - 알고리즘이란 (0) | 2020.12.25 |



